CC BY 4.0 (除特别声明或转载文章外)
如果这篇博客帮助到你,可以请我喝一杯咖啡~
处理动机
在测试代码的性能时,一般常用的测试函数大部分的最小值都在0附近,为了防止代码的设计上偏向于将最小值取向0,保证测试的准确性,便有了测试函数的一些平移和旋转处理。
具体流程
在测试函数对种群中各个个体进行处理时,所输入的个体都是一系列的行向量,所以可以参考线性变换的方式对所有参与测试的行向量在进行测试之前经过统一的处理。
首先生成一个随机的偏移向量,向量的长度与被测向量的长度相同,对两个向量进行相加得到偏移之后的向量。
然后生成一个随机的行向量与被测向量长度相同,对其使用diag函数化成对角矩阵,该矩阵即是所需的旋转矩阵,将偏移后的向量与旋转矩阵相乘,便可以得到进行处理后的向量。
因为对所有的向量进行的操作都是统一的,所以对最终的函数求解不会产生影响。
代码实现
为了方便理解,我使用了最基础的DE算法,代码中的test变量即为处理之后的输入向量
变量M为旋转矩阵,shift为偏移向量。下面是代码实现以及运行图像,其中所用到的测试函数在之前的博客中有写, 如有需要请点击SaDE
close all;
clear all;
clc;
cecnum=1;
NP=50; %种群数量
CR=0.1; %交叉概率
F=0.5; %变异算子
G=500; %迭代次数
D=30; %染色体长度
a=-5; %下限
b=5; %上限
x=zeros(NP,D); %分别生成三个NP*D的0矩阵
V=zeros(NP,D);
u=zeros(NP,D);
x=rand(NP,D)*(b-a)+a; %初始化初始种群
xuanzhuan = rand(1, D);
M=diag(xuanzhuan);
shift=rand(1,D);
for i=1:1:NP %种群中所有个体适应度的计算
test=(x(i,:)+shift)*M;
ob(i)=cec17(test,cecnum);
end
trace(1)=min(ob); %取种群中适应度最高的个体,即函数值最小的点
for g=1:1:G %在初始种群中随机取三个个体进行变异操作,并保证三个个体互相不同
for m=1:1:NP
r1=randi([1,NP],1,1);
while (r1==m)
r1=randi([1,NP],1,1);
end
r2=randi([1,NP],1,1);
while(r1==r2)||(r2==m)
r2=randi([1,NP],1,1);
end
r3=randi([1,NP],1,1);
while(r3==m)||(r3==r2)||(r3==r1)
r3=randi([1,NP],1,1);
end
v(m,:)=x(r1,:)+F*(x(r2,:)-x(r3,:)); %变异操作
end
r=randi([1,D],1,1); %随机取一个染色体位置,使该位置必定交叉,目的是为了防止接下来的交叉环节未交叉任何染色体
for n=1:1:D %该操作是针对所有个体的同一染色体
cr=rand;
if(cr<=CR)||(n==r) %根据交叉概率进行随机交叉
u(:,n)=v(:,n);
else
u(:,n)=x(:,n);
end
end
for m=1:1:NP %上下限判断,防止数据范围超出题目所给范围
for n=1:1:D
if u(m,n)<=a
u(m,n)=a;
end
if u(m,n)>=b
u(m,n)=b;
end
end
end
for m=1:NP %重新计算所有新个体适应度
test=(u(m,:)+shift)*M;
ob_1(m)=cec17(test,cecnum);
end
for m=1:1:NP %比较新老种群的适应度,优胜劣汰
if ob_1(m)<ob(m);
x(m,:)=u(m,:);
end
end
for m=1:1:NP %重新计算最小适应度
test=(x(m,:)+shift)*M;
ob(m)=cec17(test,cecnum);
end
trace(g+1)=min(ob);
tt=min(ob);
end
x(1,:);
figure(1);
plot(trace);
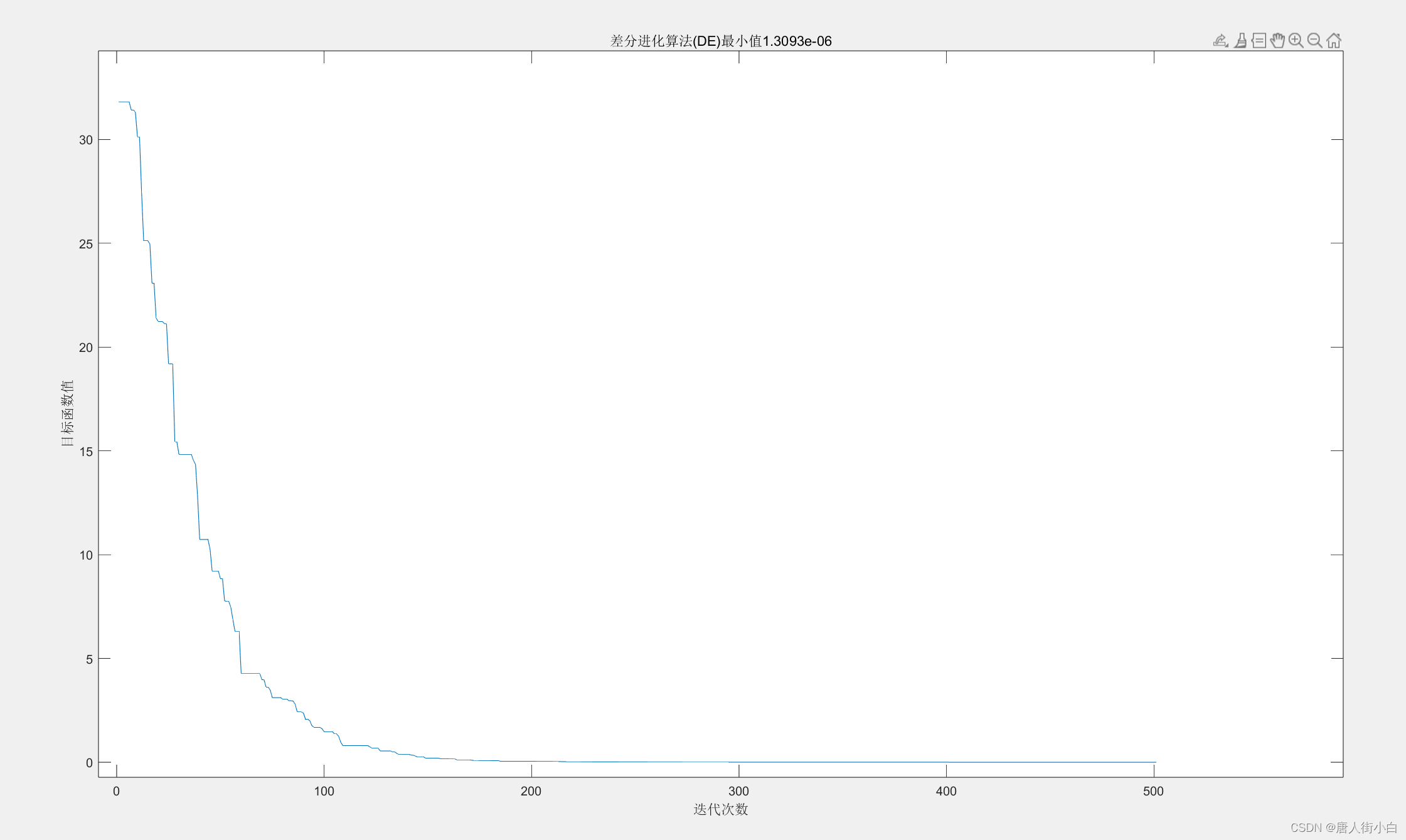
title(['差分进化算法(DE)','最小值',num2str(tt)]);
xlabel('迭代次数');
ylabel('目标函数值');
上述代码的运行结果